Atenție: e un articol destul de lung fiindcă am încercat să punem toate funcțiile în el. S-ar putea să te plictisești, amețești sau să cedezi (funcțiile sunt bătaie mare de cap, mai ales că se dau la bac), așa că respiră adânc și citește/rezolvă cu atenție.
Definiție: Fiind date două mulțimi A – domeniul de definiție și B- codomeniul (domeniul de valori), o relație f:AB este o funcție dacă: x A, unic y B, astfel incat f(x)=y.
Reprezentarea grafică:
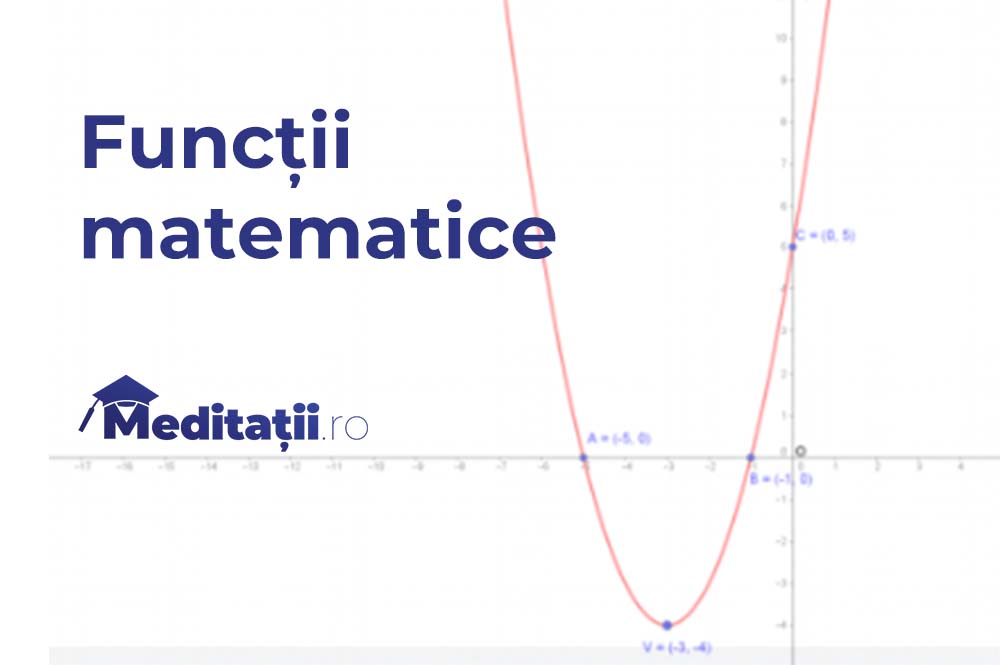
Pentru funcția 𝑓: 𝑅 → 𝑅, 𝑓(𝑥) = x2+6x+5.
Alcatuim tabelul de variatie:
| 𝑥 | – | −5 | -3 | -1 | 0 | |
| 𝑓(𝑥) | 0 | -4 | 0 | 5 |
Astfel, graficul funcției va fi:
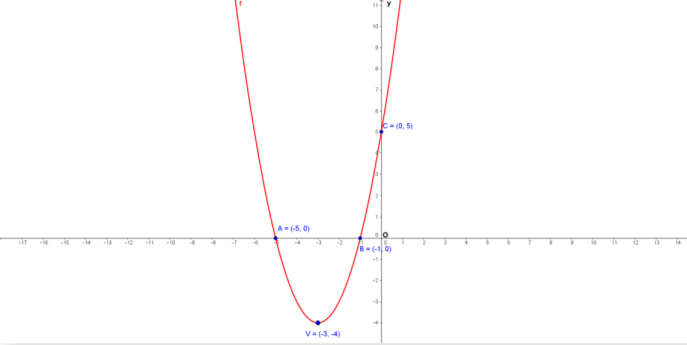
Este util de reținut poziția graficului 𝐺 față de axa 𝑂𝑥:
• 𝐺 se află „deasupra” axei 𝑂𝑥 ⟺ 𝑓(𝑥) > 0, ∀𝑥 ∈ 𝐸
• 𝐺 intersectează axa 𝑂𝑥 în (𝑎, 0) ⟺ 𝑓(𝑥) = 0
• 𝐺 se află „sub” axa 𝑂𝑥 ⟺ 𝑓(𝑥) < 0, ∀𝑥 ∈ 𝐸
Monotonia
Pentru funcția 𝑓: 𝐸 → 𝑅 și I o submulțime a lui E:
• 𝑓 este strict crescătoare pe 𝐼 dacă 𝑥, 𝑦 ∈ 𝐼, 𝑥 < 𝑦 ⟹ 𝑓(𝑥) < 𝑓(𝑦)
• 𝑓 este strict descrescătoare pe 𝐼 dacă 𝑥, 𝑦 ∈ 𝐼, 𝑥 < 𝑦 ⟹ 𝑓(𝑥) > 𝑓(𝑦)
• f este strict monotonă pe 𝐼 dacă este strict crescătoare sau strict descrescătoare pe 𝐼.
Exemplu:
Intervalele de monotonie pentru funcția 𝑓: 𝑅 → 𝑅, 𝑓(𝑥) = x2+6x+5sunt:
• pe (−∞, −3) funcția este strict descrescătoare
• pe (−3, ∞) funcția este strict crescătoare
Intervalele de convexitate (concavitate)
Funcția 𝑓: 𝐸 → 𝑅 și 𝐼 ⊆ 𝐸 este convexă pe I (respectiv concavă pe I) dacă pentru orice 𝑎, 𝑏 ∈ 𝐼, 𝑎 < 𝑏 și punctele 𝐴(𝑎, 𝑓(𝑎)),𝐵(𝑏, 𝑓(𝑏)), reprezentarea grafică a lui 𝑓 pe [𝑎, 𝑏] se află sub segmentul AB (respectiv deasupra segmentului AB).

Proprietăți ale funcțiilor:
- Funcții injective
Fie functia 𝑓: 𝐴 → 𝐵, 𝐴, 𝐵 ⊆ 𝑅. Funcția 𝑓: 𝐴 → 𝐵 se numește funcție injectivă sau injecție dacă orice două elemente distincte din 𝐴 au imagini distincte în 𝐵
Faptul că funcția 𝑓: 𝐴 → 𝐵 este injectivă se mai poate exprima
i) ∀x1, x2 A, x1x2 f(x1)f(x2)
ii) ∀x1, x2 A, f(x1)=f(x2) x1= x2
Exemple:
1. Arătați că 𝑓: 𝑅 → 𝑅, 𝑓(𝑥) = 2𝑥 + 3 este injectivă.
Din proprietatea ii):
∀x1, x2 A, f(x1)=f(x2) 2×1 + 3 = 2×2 + 3 ⟹ x1=x2, deci funcția este injectivă.
2. Arătați că 𝑓: 𝑅 → 𝑅, 𝑓(𝑥) = x2+3x+2 nu este o injecție.
𝑓(𝑥) = x2+3x+2= 𝑥(𝑥 + 2) + 3.
Luăm x1 = 0, x2=-2
Observăm că x1 ≠ x2, dar 𝑓(x1) = 𝑓(0) = 3 și 𝑓(x2) = 𝑓(−2) = 3 ⟹ f(x1)=f(x2), deci funcția nu este injectivă.
Interpretarea geometrică a injectivității unei funcții
Dacă orice paralelă cu axa 𝑂𝑥 intersectează graficul funcției numerice 𝑓: 𝐴 → 𝐵 în cel mult un punct, atunci f este injectivă.
Exercițiu:
Arătați ca funcția 𝑓: 𝑅 → 𝑅

nu este injectivă.
Facem tabelul de variație al funcției pentru a-i trasa graficul. Având în vedere că funcția este compusă, facem câte un tabel de variație pentru fiecare ramură.

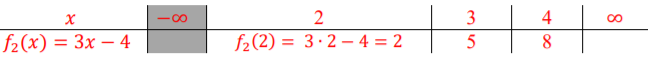
Graficele le vom trasa în același sistem de axe de coordonate 𝑥𝑂𝑦 și vom duce două paralele la axa 𝑂𝑥, una 𝑦 = 2,5 și cealaltă 𝑦 = −2.
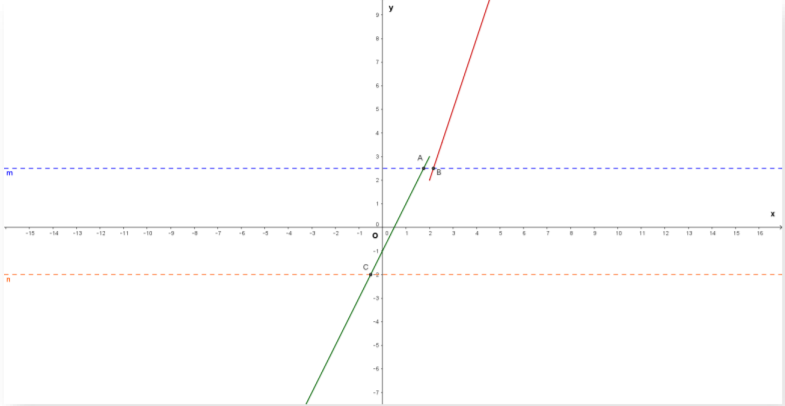
Observăm că dreapta 𝑦 = 2,5 intersectează graficul în două puncte, deci funcția nu este injectivă.
Legatura dintre injectivitate si monotonie:
Fie 𝑓: 𝑅 → 𝑅 o funcție numerică.
i) dacă f este strict monotonă, atunci f este injectivă;
ii) dacă f este injectivă, nu rezultă în mod necesar că f este strict monotonă
iii) dacă f nu este injectivă, atunci f nu este strict monotonă.

- funcții surjective
Funcția 𝑓: 𝐴 → 𝐵 se numește funcție surjectivă sau surjecție dacă orice element din codomeniul 𝐵 este imaginea cel puțin unui element din domeniul de definiție 𝐴 prin funcția 𝑓.
Faptul că 𝑓: 𝐴 → 𝐵 este surjectivă se poate exprima astfel:
∀𝑦 ∈ 𝐵, ∃𝑥 ∈ 𝐴 astfel încât 𝑦 = 𝑓(𝑥)
Exemplu:
Arătăm că funcția 𝑓: 𝑅 → [0, ∞), 𝑓(𝑥) = x2 este surjectivă.
Pornind de la definiție,
∀y ∈ [0, ∞), ∃𝑥 ∈ 𝑅 astfel încât 𝑦 = 𝑓(𝑥),
obținem 𝑦 = x2 ⟹ 𝑥 = ±y. Deci, 𝑓(𝑥) = 𝑓(±y) = (±y)2 = 𝑦, deci funcția este surjectivă.
Interpretarea geometrică a surjectivității unei funcții
Dacă orice dreaptă paralelă la axa 𝑂𝑥, 𝑦 = 𝑏, 𝑏 ∈ 𝐵, intersectează graficul funcției în cel puțin un punct, atunci funcția numerică 𝑓: 𝐴 → 𝐵 este surjectivă.
Exemplu:
1. Arătați ca funcția 𝑓: 𝑅 → 𝑅
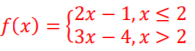
este surjectivă.
Uitandu-ne pe graficul trasat mai sus, observăm că orice paralelă dusă la axa 𝑂𝑥 intersectează graficul în unul sau două puncte, deci concluzia este că funcția dată este surjectivă.
2. Fie functia 𝑓: 𝑅 → 𝑅, 𝑓(𝑥) = |𝑥 + 2| + 4. Arătați ca funcția nu e surjectiva.
În primul rand explicitam modulul. f devine:
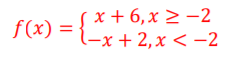
Apoi, vom studia surjectivitatea funcției folosindu-ne de interpretarea geometrică. Pentru acest lucru, începem cu tabelul de variație:
| 𝑥 | – | -4 | -3 | -2 | 0 | 1 | |
| f1 (𝑥) = 𝑥 + 6 | – | – | – | 4 | 6 | 7 | |
| f2 (𝑥) = −𝑥 + 2 | 6 | 5 | 4 | – | – | – |
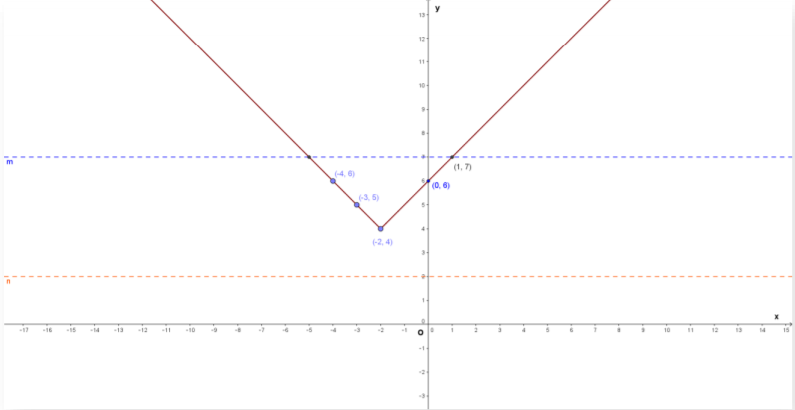
Observăm că y = 2 nu intersectează funcția în niciun punct, asadar f nu este surjectiva.
- funcții bijective
Funcția 𝑓: 𝐴 → 𝐵 se numește funcție bijectivă dacă și numai dacă este simultan injectivă și surjectivă.
Exemplu:
Arătați că funcția 𝑓: 𝑅 → 𝑅, 𝑓(𝑥) = 4𝑥 − 3 este bijectivă. Pentru a verifica bijectivitatea funcției, vom verifica mai întâi injectivitatea și apoi surjectivitatea.
Injectivitatea ∀x1, x2 A, f(x1)=f(x2) ⟹ 4×1 − 3 = 4×2 − 3 ⟹ x1 = x2, deci funcția este injectivă (1)
Surjectivitatea ∀𝑦 ∈ 𝑅, ∃𝑥 ∈ 𝑅 astfel încât 𝑦 = 𝑓(𝑥). Pornind de la 𝑦 = 4𝑥 − 3 ⟹ 𝑥 =y+34 . Deci, 𝑓(𝑥) = 𝑓 (y+34) = 𝑦 ⟹ funcția este surjectivă (2)
Din (1) și (2) rezultă că funcția este bijectivă.
Interpretarea geometrică
Dacă orice paralelă cu axa 𝑂𝑥 intersectează graficul funcției 𝑓: 𝐴 → 𝐵, într-un singur punct, atunci f este bijectivă.
- funcții inversabile
O funcție 𝑓: 𝐸 → 𝐹, unde 𝐸, 𝐹 ⊆ 𝑅, se numește funcție inversabilă dacă: există o funcție 𝑔: 𝐹 → 𝐸 care verifică relațiile:
a) 𝑓(𝑔(𝑥)) = 𝑥, ∀𝑥 ∈ 𝐹
b) 𝑔(𝑓(𝑥)) = 𝑥, ∀𝑥 ∈ 𝐸
O funcție 𝑓: 𝐸 → 𝐹 este inversabilă dacă și numai dacă este bijectivă.
Observație. Dacă funcția numerică 𝑓: 𝐸 → 𝐹 este inversabilă, atunci reprezentările grafice ale funcțiilor 𝑓 și 𝑓 −1 sunt simetrice în raport cu dreapta de ecuație 𝒚 = 𝒙 (bisectoarea cadranelor I și III)
Exemplu:
Să se arate că funcția 𝑓: 𝑅 ∖ {1} → 𝑅 ∖ {1}, definită astfel 𝑓(𝑥) = x+1x-1 este bijectivă și să se afle inversa sa.
Pentru a arăta că f este bijectivă vom arăta mai întâi că este injectivă și apoi surjectivă.
Injectivitatea ∀x1, x2 𝑅 ∖ {1}, f(x1)=f(x2) ⟹ x1+1×1-1 = x2+1×2-1 ⟹ x1x2 +x2-x1-1 =x1x2 +x1-x2-1 După reducerea termenilor asemenea, vom obține x1=x2, adică funcția este injectivă(1)
Surjectivitatea ∀𝑦 ∈ 𝑅 ∖ {1}, ∃𝑥 ∈ 𝑅 ∖ {1} astfel încât 𝑦 = 𝑓(𝑥). Într-adevăr, rezolvând ecuația 𝑦 = x+1x-1în raport cu 𝑥, vom obține 𝑥 =y+1y-1 , deci 𝑓(𝑥) = 𝑓 (y+1y-1 ) = 𝑦, adică funcția este surjectivă(2)
Din (1) și (2) rezultă că f este bijectivă. Funcția fiind bijectivă, este inversabilă și inversa ei va fi funcția: 𝑔: 𝑅 ∖ {1} → 𝑅 ∖ {1}, 𝑔(𝑦) = y+1y-1 . Revenind la notația standard, inversa funcției f este funcția: f-1 : 𝑅 ∖ {1} → 𝑅 ∖ {1}, f-1 (𝑥) = x+1x-1 .
Funcţia putere cu exponent natural, 𝒇: 𝑹 → 𝑫, 𝒇(𝒙) = xn şi 𝒏 ∈ N*.
Proprietățile funcției putere
- Graficul funcției putere se intersectează cu axele de coordonate în punctul 𝑂(0,0).
- Funcția putere cu exponent natural 𝑛 (𝑛 = 2𝑘) este funcție pară.
Funcția putere cu exponent natural 𝑛 (𝑛 = 2𝑘 + 1) este funcție impară
2.1. Să verificăm paritatea funcției 𝒇: 𝑅 → 𝐷, 𝑓(𝑥) = x2 .
Soluție. Deoarece 𝑓(−𝑥) = (-x)2 = x2 = 𝑓(𝑥) funcția este pară.
2.2. Să verificăm paritatea funcției 𝒇: 𝑅 → 𝐷, 𝑓(𝑥) = x3 .
Soluție. Deoarece 𝑓(−𝑥) = (-x)3 = -x3 = −𝑓(𝑥) funcția este impară.
3. Graficul funcției putere cu exponent natural 𝑛 (𝑛 = 2𝑘) este simetric față de axa 𝑂𝑦.
Graficul funcției putere cu exponent natural 𝑛 (𝑛 = 2𝑘 + 1) este simetric față de 𝑂(0,0).
4. Funcția putere cu exponent natural 𝑛 (𝑛 = 2𝑘) este o funcție convexă.
Funcția putere cu exponent natural 𝑛 (𝑛 = 2𝑘 + 1) este:
• funcție convexă pe intervalul [0, ∞);
• funcție concavă pe intervalul (−∞, 0];
• 𝑂(0,0) este punct de inflexiune.
5. Monotonia functiei putere cu exponent natural 𝑛 (𝑛 = 2𝑘):
• este descrescătoare pe intervalul (−∞, 0]
• este crescătoare pe intervalul [0, ∞)
• punctul (0,0) este punct de minim
Funcția putere cu exponent natural 𝑛 (𝑛 = 2𝑘 + 1) este strict crescătoare pe 𝑅.
Trasand graficul funcției f(x)=x2 se observa toate proprietățile pentru n=2k.
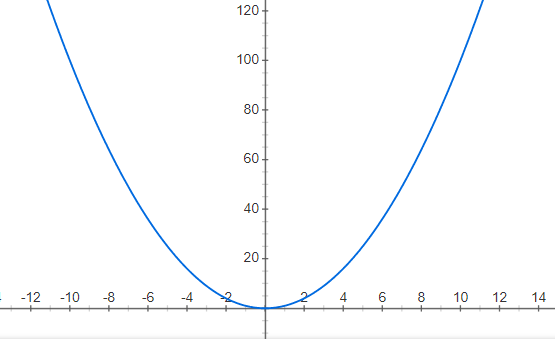
Trasand graficul funcției f(x)=x3 se observa toate proprietățile pentru n=2k+1.

IV. Funcția radical 𝒇: 𝑹 → 𝑫, 𝒇(𝒙) = nx şi 𝒏 ∈ N*
Proprietatile functiei radical:
- Graficul funcției radical se intersectează cu axele de coordonate în punctul 𝑂(0,0).
- Funcția radical de ordin impar (𝑛 = 2𝑘+1) este funcție impara.
- Funcția radical este strict crescătoare (și pentru n par și pentru n impar).
- Funcția radical este bijectiva (și pentru n par și pentru n impar).
- Funcția radical de ordin par (𝑛 = 2𝑘) este concavă.
Funcția radical de ordin impar (𝑛 = 2𝑘+1) este convexă pe (-, 0] și este concavă pe [0, ).

Funcția radical de ordin 2 este definită doar pe [0, ) (la fel ca toate funcțiile radical de ordin par).

Funcția radical de ordin 3 este definită doar pe R (la fel ca toate funcțiile radical de ordin impar).
FUNCȚIA EXPONENȚIALĂ
Definiție: O funcție f:R, f(x) = ax, a > 0, a1se numeste funcție exponențială.
Proprietăți
1. Funcția exponentiala este bijectiva.
2. Funcția exponentiala este inversabilă, inversa funcției este functia logaritmica.
3. Functia exponentiala este strict crescătoare pentru a>1 si strict descrescatoare pentru 0 <a<1.
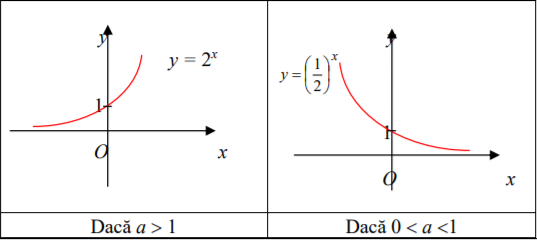
Funcția logaritmică
Fie a>0, a1; funcția f:(0, )R, f(x) = logax se numeste functia logaritmica de baza a.
Proprietăți:
- f(1)=0
- functia logaritmica este strict crescătoare pentru a>1 și este strict descrescătoare pentru 0 <a<1.
- functia logaritmica este bijectiva (deci inversabila), iar inversa ei este functia exponentiala.

Ecuații iraționale
- Radicali de ordin par
parf(x)=g(x) Condiții de existență: f(x) 0, g(x) 0
(atat rezultatul, cat și expresia de sub radical trebuie sa fie pozitive)
- Radicali de ordin impar
imparf(x)=g(x) Nu sunt necesare condiții de existență;
- Ecuatii irationale ( adică nu conțin necunoscuta și sub radical)
Etapele rezolvării:
- Condițiile de existenta (pentru radicalii de ordin par)
- Rezolvare – ridicarea ecuatiei la putere egala cu ordinul radicalului
- Verificare: a.(pt. radicalii de ordin par) dacă soluția satisface condițiile de existență
b. inlocuire direct în ecuația inițială
Exemple
- x-3=3-x
Condiții: x-30x3x[3, )
3-x03xx(-, 3]
x-3=3-x /2 (x-3)2=(3-x)2 x-3=9-6x+x2
x2-6x+9-x+3=0x2-7x+12=0
x2-7x+12=0, rezolvam ecuatia de gradul II
=72-412=49-48=1
x1, 2=712 x {3, 4}
Verificand condițiile de existență ramane soluția unică x=3.
- 34x-8=2
Nu sunt necesare condiții de existență intrucat ordinul radicalului este număr impar (3).
34x-8=2/3(34x-8)3=23 4x-8=8 4x=16x=4
Așadar, soluția ecuatiei este x=4.
Exemple:
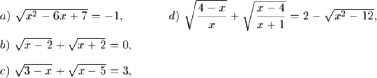
Rezolvare:
a) Se observă că membrul din dreapta ecuatiei este negativ, pe cand cel din stanga, fiind un radical de ordinul doi, poate primi doar valori nenegative (mai mari sau egale cu 0). Așadar ecuația nu are soluții.
b) Cum suma a două expresii, valorile cărora sunt numere negative, este egal cu zero, rezultă că ambele expresii concomitent sunt egale cu zero. Așadar, ecuația este echivalentă cu sistemul de ecuații care este incompatibil. Prin urmare, ecuația nu are soluții.
| x-2 = 0 x+2 = 0 |
c) Domeniul valorilor (DV) ecuatiei se determina din sistemul (expresiile ce se conțin sub semnul radicalului de ordinul doi urmează a fi nenegative). Evident sistemul nu are soluții, și, prin urmare, ecuația la fel nu are soluție.
| 3-x >= 0 x-5 >= 0 |
d) Domeniul valorilor ecuatiei se determina rezolvând sistemul
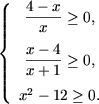
Cum x=4 este unica valoare admisibila a ecuatiei, ramane de verificat, dacă ea este sau nu soluție a ecuației. Introducand in ecuatie x=4 se obține egalitatea 0 = 0 și, prin urmare, x = 4 este unica soluție a ecuației date.
FUNCȚII TRIGONOMETRICE INVERSE
arcsin
Restricția funcției sin la intervalul [-2, 2] este bijectiva, deci inversabila. Definim funcția inversa
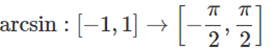
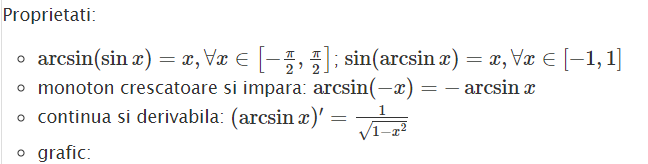

arccos
Restricția funcției cos la intervalul [0,π] este bijectiva, deci inversabila. Definim funcția inversa
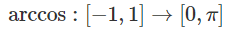
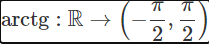
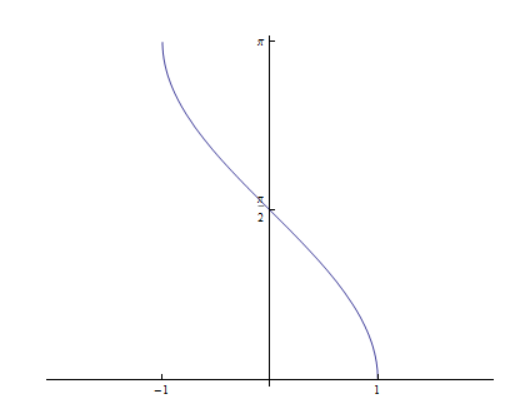
arctg
Restricția funcției tg la intervalul [-2, 2] este bijectiva, deci inversabila. Definim funcția inversa

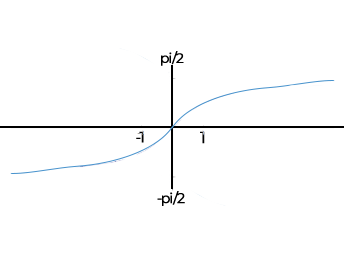
arcctg
Restricția funcției cos la intervalul [0,π] este bijectiva, deci inversabila. Definim funcția inversa



Ecuatii exponentiale ( cu necunoscuta situata la exponent)
Tipuri de ecuații
- ecuații de tipul ax=b, a>0, a1, b>0
Se logaritmeaza, de obicei, în baza a.
exemplu 1: 2x=16 2x =24x=4
exemplu 2: 2x=3 / log2 log22x = log23 (exponentul lui 2 trece in fata logaritmului) xlog22 = log23 x=log23
- ecuații de tipul af(x)=b, a>0, a1, b>0
Se rezolva la fel ca și 1.
exemplu 1: 35x-2=935x-2=325x-2=25x=4x=54
exemplu 2: 35x-2=7 /log3 log335x-2=log37 (5x-2) log33 = log37 5x- 2=log37 5x=log37+2x=log37+25
- ecuații în care se repeta puterea
2x+2x-1+2x+1=56; încercăm să obținem în fiecare membru al sumei 2x
2x+2x-1+2x+1=562x+2x:2+2×2=56 2x(1+12+2)=562x(22+12+42)=56
2×2+1+42=562×7=5622x=11272x=16x=4
- ecuații care în urma unor substituții devin algebrice
exemplu: 4x-2x=12(2x)2-2x=12 ( facem substitutia 2x=t)
t2-t-12=0 – ecuatie de gradul II
=(-1)2-4(-12) = 1+48=49
t1, 2=1492=172 t{4, -3}
Revenind la substituție : 2x=4 x=2, apoi 2x=-3 și e Imposibil
Exerciții:
- Sa se rezolve ecuatiile
a) 2x=-4, b) 2x=4, c)2x=5.
Rezolvare:
a) Cum membrul din stanga ecuatiei este pozitiv pentru orice x ∈ R (a se vedea proprietatile functiei exponentiale), iar membrul din dreapta este negativ, ecuația nu are soluții.
b) Utilizând tipul 1 de ecuații logaritmice se obține x=log24, adică x=2.
c) Similar exemplului precedent se obține x=log25.
- Sa se rezolve ecuatiile
a) 2sin x = 12
b) 3|x2-x|=9
c) (5) 2+4+6+…+2x = 545, x N


Ecuatii logaritmice – conțin necunoscută în logaritm
Tipuri de ecuații logaritmice:
ecuații de tipul logax=b, a>0, a1, b aparțin de R
Se impun condițiile de existență: x>0;
Apoi logax=bx=ab
exemplu: log2x=4; Condiții: x>0x(0, )
log2x=4x=24x=16 (0, )
ecuații de tipul loga f(x) = b, a > 0, a1, b aparțin de R
Se impun condițiile de existență: f(x) > 0 ∀ xD,D= domeniul de definiție a lui x
Apoi loga f(x)=bab=f(x) și se rezolva ecuatia
exemplu: log2(2x-4)=2; Condiții: 2x-4>0x>2x(2, )
log3(2x-4)=22x-4=322x=13x=132(2, )
ecuații de tipul logaf(x) = logbg(x), a>0, a1
Se impun condițiile de existență: f(x)>0 si g(x)>0
Apoi se rezolva ecuatia: f(x)=g(x)
exemplu: log2(x-3)=log2(5-x);
Condiții: x-3>0x>3x(3, )
5-x>0x<5x(-, 5)
făcând reuniunea intervalelor x(3,5)
x-3=5-x2x=8x=4(3, 5)
ecuații în care se utilizează proprietăți ale logaritmilor și apoi ajungem la ecuații de tipul 1, 2, 3.
exemplu: lg(x+1)-lg 9 = 1-lg x;
Condiții: x+1>0x>-1x(-1, )
x>0x(0, )
reunind intervalele x(0, )
Apoi: lgx+19=lg 10-lg xlgx+19=lg10xx+19=10xx(x+1)=90
x2+x-90=0=12-4(-90)=361=192×1, 2=-1192x{-10, 9}
ținând cont de condițiile de existență x=9
ecuații care în urma unor substituții devin ecuații algebrice
exemplu: lg2 x +5lg x -6=0(lg x)2 + 5 (lg x)-6=0;
Condiții: x>0x(0, )
Notăm: lg x =t, tRecuația devine: t2+5t-6=0
=52-46=1
x1, 2=-512x{1, -6}R
Revenind la substituție:
- lg x=1x=10
- lgx=-6x=10-6
Așadar multimea solutiilor este S={10, 10-6}






Sper că ți-a fost de ajutor, iar dacă vrei să te pregătești în detaliu la matematică nu ezita să folosești profesorii noștri de top de pe https://meditatii.ro/matematica/online