Pentru a explica conceptele legate de vectori într-un mod accesibil, haideți să folosim niște analogii și exemple din viața reală, asemănător cu cele create pentru structurile de codificare în informatică.
Direcția și Segmentele Orientate: Imaginați-vă că vă aflați într-un parc și priviți către diferite obiective – de exemplu, de la punctul unde sunteți (punctul A) către un copac (punctul B). Traseul pe care l-ați urma de la A la B reprezintă un segment orientat. Dacă o altă persoană ar urma exact același traseu de la un alt punct de plecare, dar în aceeași direcție către un alt copac aflat în linie dreaptă cu traseul dvs., atunci cele două trasee ar avea aceeași direcție.
Vectorii și Echipolența (când doi sau mai mulți vectori au aceleași caracteristici fundamentale: aceeași lungime, aceeași direcție și același sens): Să ne imaginăm că traseul de la A la B este un drum pe care îl parcurgem cu bicicleta. Dacă un prieten parcurge un drum de aceeași lungime, în aceeași direcție și cu bicicleta, chiar dacă startul este într-un alt loc, ambele trasee sunt echivalente din perspectiva noastră – ele sunt ca doi vectori echipolenți. Asta înseamnă că, în esență, am parcurs “același drum” în termeni de efort și destinație relativă, chiar dacă punctele de start și de sfârșit sunt diferite.
Vectori Egali și Opuși: Dacă eu și tu pornim din același loc și mergem exact în aceeași direcție și distanță, traseele noastre reprezintă doi vectori egali. Însă, dacă tu te-ai întoarce și ai merge în direcția opusă pentru aceeași distanță, traseele noastre ar reprezenta vectori opuși: am parcurs aceeași distanță, dar în direcții complet diferite.
Adunarea Vectorilor: Închipuiți-vă acum că traseul de la A la B este primul vector și decideți să mergeți mai departe către un alt punct C, creând astfel un al doilea vector. Dacă desenăm aceste trasee pe o hartă, putem forma un paralelogram, iar traseul cel mai direct de la punctul de start (A) la ultimul punct de oprire (C) ar fi diagonala acestui paralelogram. Acest traseu direct de la A la C reprezintă suma celor doi vectori – adică, cel mai eficient mod de a combina cele două “etape” ale călătoriei într-una singură.
Acum că am mai înțeles despre ce e vorba, hai să o luăm și matematic:
Se numește direcție a dreptei d mulțimea formată din dreapta d și din toate dreptele paralele cu d. Spunem că două segmente au aceeași direcție dacă dreptele lor suport sunt paralele sau coincid. O pereche ordonată de puncte (A,B) din plan se numește segment orientat.
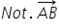
A – se numește originea sau punctul de aplicație
B – se numește extremitatea segmentului orientat sau vârf.
Lungimea segmentului [AB] se numește modulul segmentului orientat.
Două segmente orientate se numesc echipolente dacă au aceeasi mărime (modul), direcție și sens.
Se numește vector mulțimea tuturor segmentelor orientate echipolente cu un segment orientat dat. Se numește versor sau vector unitate, vectorul având lungimea egală cu 1.
! Observație 1: Doi vectori sunt egali dacă au aceeași mărime, direcție și sens.
! Observație 2: Doi vectori sunt opuși dacă au aceeași mărime și direcție, dar sensuri opuse.
Adunarea vectorilor după regula paralelogramului
Se așează cei doi vectori astfel încât să aibă originea în același punct. Se constuiește un paralelogram ducând paralele la cei doi vectori prin vârfurile lor. Vectorul sumă va fi diagonala paralelogramului cu originea în originea comună a celor doi vectori.

Adunarea vectorilor după regula triunghiului
Se așează al doilea vector cu originea în vârful primului vector. Vectorul sumă va fi vectorul cu originea în originea primului vector și cu extremitatea în extremitatea celui de-al doilea vector.

Adunarea vectorilor după regula poligonului
Se așează vectorii succesiv unul cu originea în vârful celuilalt. Vectorul sumă va fi vectorul cu originea în originea primului vector și cu extremitatea în extremitatea ultimului vector.
Proprietățile adunării vectorilor
Asociativitatea:

Comutativitatea:
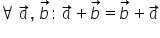
Elementul neutru- vectorul nul:
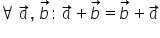
Elementul opus (vectorul opus):
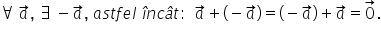
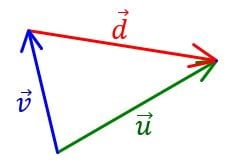
Pentru a obține vectorul diferență, se așează cei doi vectori astfel încât să aibă originea comună. Vectorul diferență este vectorul având originea în extremitatea scăzătorului și vârful în extremitatea descăzutului.
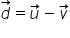

Proprietățile înmulțirii unui vector cu un scalar
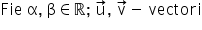
Înmulțirea cu scalari este distributivă față de adunarea vectorilor
Înmulțirea cu scalari este distributivă față de adunarea scalarilor
Asociativitatea înmulțirii scalarilor
Numărul 1 este element neutru pentru înmulțirea vectorilor cu scalari
Cazuri particulare:

O pereche ordonată de axe perpendiculare având aceeași origine formează un reper cartezian ortogonal. Punctul O se numește originea reperului. Axa Ox se numește axa absciselor, iar Oy axa ordonatelor. Pe cele două axe vom considera versorii
Fie A și B două puncte în plan având coordonatele:
Atunci vectorul se descompune după direcțiile date de cei doi versori astfel:
Vectorul se descompune după direcțiile date de cei doi versori astfel:
Modulul vectorului AB este:
Proprietăți


Vectori de poziție
Definiție. Fie O un punct fixat în plan și A un alt punct din plan. Atunci vectorul se numește vector de poziție al punctului A.
Notație:
Dacă A și B sunt puncte în plan, atunci are loc relația:
Vectorul de poziție al unui punct care împarte un segment într-un raport dat
În particular, dacă k = 1, atunci M este mijlocul segmentului [AB], iar vectorul de poziție al punctului M va fi:

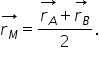
Fie ABC un triunghi și G centrul de greutate al triunghiului (punctul de intersecție al medianelor). Vectorul de poziție al punctului G este:
Proprietate:

Sper că ți-a fost de ajutor, iar dacă vrei să te pregătești în detaliu la matematică nu ezita să folosești profesorii noștri de top de pe https://meditatii.ro/matematica/online.
Meditatii matematica pentru toate nivelurile, de la scoala primara, gimnaziu, liceu, admitere, facultate, master sau doctorat in locatii din Romania. Meditatii Matematica in Bucuresti sau Meditatii Matematica Bacalaureat pe Meditatii.ro



